Introduction
Ever since its discovery in 1965, the Cosmic Microwave Background (CMB) (Penzias & Wilson (1965)) has proven to be a scientific goldmine in Cosmology. It constitutes one of the main pillars of the Lambda Cold Dark Matter (ΛCDM) model (Zyla et al. (2020)), allowing for a very high-precision measurement of its free parameters (Hinshaw et al. (2013); Planck Collaboration (2020a)). This model describes the evolution of our universe from an initial high energy state. It has been very successful in predicting many phenomena, such as nucleosynthesis or the expansion of the universe. Nevertheless, there are some questions, such as the Horizon Problem or the Flatness Problem (see Watson (2000) for a detailed exposition), not explained by it.
Inflationary theories (see Martin et al. (2014) for a compendium of these, or Guth (1981) for the original reference) solve for these unknowns by proposing a period in the very early universe in which the universe expanded by a factor of at least e60. Inflation is nowadays considered as an extension of the Big Bang theory. The recent new maps of the CMB, produced, for example, by the Wilkinson Microwave Anisotropy Probe (WMAP) (Bennett et al. (2003)) and the Planck Surveyor (Planck Collaboration (2011)) have provided compelling evidence that it did occur. However, there is a prediction, which remains unfound, and which would constitute ‘smoking-gun’ evidence supporting this model. If inflation took place at an energy scale of ∼ 1015 GeV or greater, as several models suggest, the gravitational waves produced during inflation could have survived long enough to leave an imprint in the CMB polarization anisotropy. Specifically, there is a parity-odd pattern in the polarization field, called a B−mode, that is uniquely sourced by gravitational waves.
Several experiments, such as the Background Imaging of Cosmic Extragalactic Polarization (BICEP)/Keck Array (BICEP/Keck Collaboration (2021)) or the Atacama B-Mode Search (ABS) (Kusaka et al. (2018)) have been searching for this gravitational signal for years, but the finding of the most distinctive signature of inflation still eludes us. As we will see, one of the difficulties that these surveys present is the fact that, at the usual CMB observing frequencies (∼ 100 GHz), the sky signal is strongly dominated by polarized foregrounds.
Inflation
After the Cosmic Background Explorer’s (COBE) measurement of the blackbody spectrum of the CMB (Mather et al. (1994)) cosmologists noticed the extreme uniformity of it’s temperature. Today, we know that the intensity deviations are of only one part in ∼ 105 across the entire sky. ΛCDM predicts the thermal initial conditions to be random at each point, but this would lead to an infimum probability of having a CMB temperature anisotropy map as the one we observe.
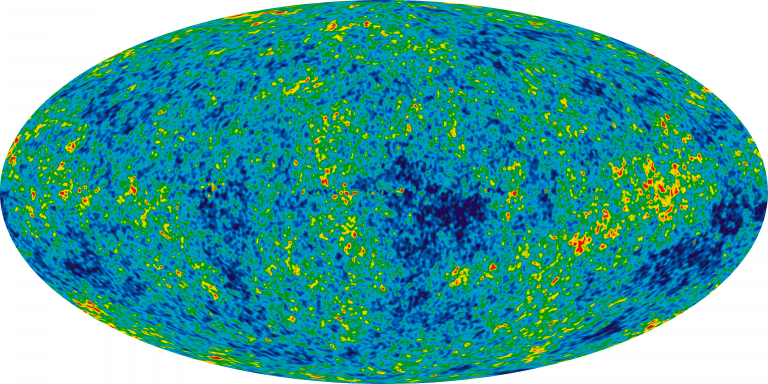
As the CMB was emitted when the universe was 380,000 years old, only points closer in distance to around 1.2◦ on the sky could have been in thermal equilibrium by the time when the CMB was produced (Dodelson (2020)). How can the CMB be so uniform then? This is known as the ‘Horizon Problem’ in cosmology. Inflation solves it by proposing an epoch of exponential expansion in the very early universe.
During inflation, the universe consists of an uniform background metric and an uniform scalar field. There are two kind of perturbations that concern us: scalar and tensor perturbations. Scalar perturbations couple to the density of radiation and matter, being responsible for the majority of inhomogeneities and anisotropies in the universe. On the other hand, tensor perturbations are perturbations in the metric itself and they propagate as gravitational waves.
CMB Polarization
In radio astronomy, polarization is usually expressed in terms of the four Stokes parameters, I (intensity), Q and U (linear polarization) and V (circular polarization) (Robishaw & Heiles (2021)). In cosmology, as there are almost no circularly polarized sources, we just focus on Stokes I, Q and U . Polarization vectors (represented in Stokes Q and U ) are spin-2 vectors, this is, a polarization vector rotated 180◦ is identical to the vector before the rotation.
We can use the formalism described in (Kamionkowski et al. (1997); Zaldarriaga & Seljak (1997)) to decompose the polarization vector field into two components, E− (parity-even) and B− (parity-odd) modes:
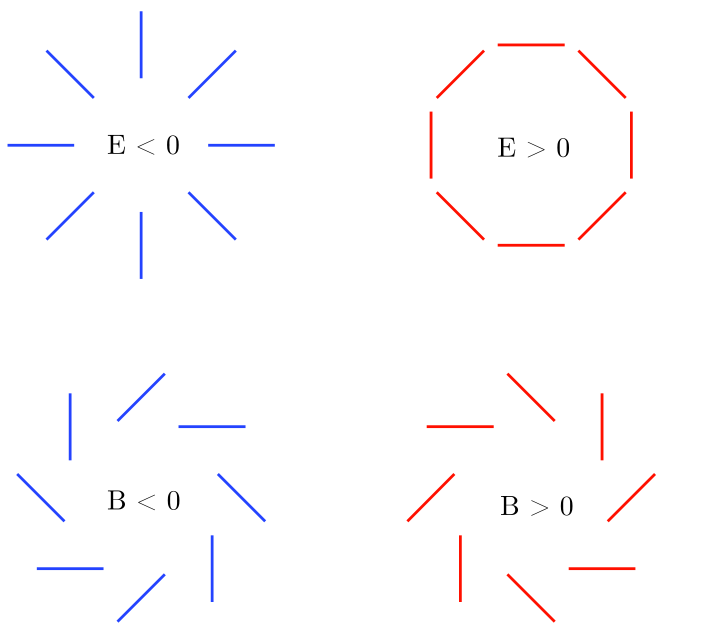
There are two important advantages of working with this decomposition. First of all, these are scalar functions, so we can use techniques such as the angular power spectra to study them. Secondly, scalar perturbations induce only E− modes, while tensor perturbations create both E− and B−modes. Therefore, finding B−modes would be a clean diagnostic of the presence of gravitational waves.
The E−mode signal has been well measured and characterized (SPT-3G Collaboration (2021)). Unfortunately, the B−mode signal is predicted to be very small, at least about 100 times smaller than the E-mode. Up to now there has not been a measurement but only constraints on B−modes.
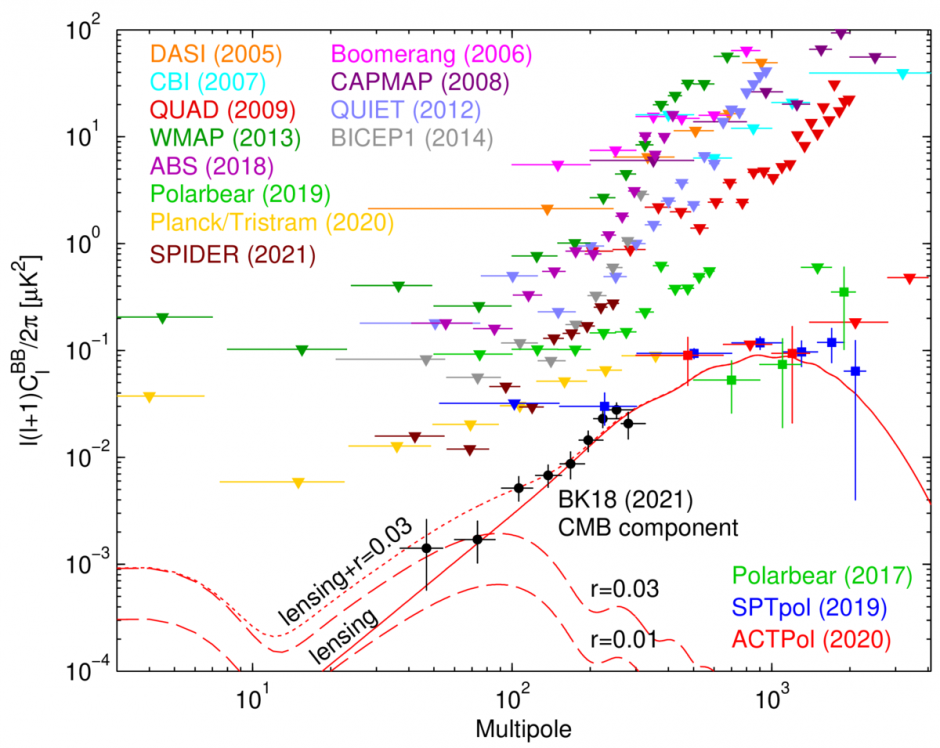
Apart from the low intensity of this signal there are several challenges that need to be faced (see (Kamionkowski & Kovetz (2016)) for a comprehensive introduction and an extensive reference list). First and foremost, foreground contamination has proven to be a very serious issue for any experiment trying to detect it. Sophisticated techniques need to be developed in order to account for these. Moreover, primordial gravitational waves are not the only way that a B-mode signal could be generated. In 2013, the SPTpol collaboration showed a detection of B−modes coming from graviational lensing (SPTpol Collaboration (2013)). Furthermore, the fact that many of the experiments searching for B− modes (BICEP, SPTpol) are only observing a part of the sky has an impact in the polarization measurements.
Foregrounds
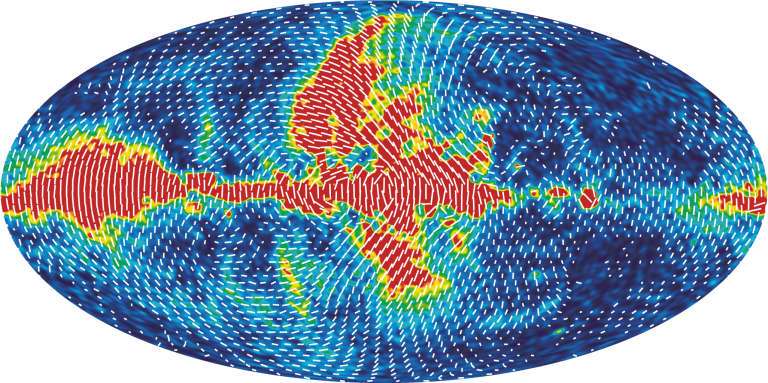
Any radiation between the CMB and a detector looking for cosmological signal is considered to be a foreground, since it can interfere with our interpretation of the observation. The majority of these foregrounds come from our Galaxy (see the latest Stokes I, Q and U maps from Planck Collaboration (2020c)), but there is also an important contribution in smaller angular scales coming from point sources, mainly extragalactic ones. For these, catalogues such as the one produced by the Atacama Cosmology Telescope (ACT) (Aiola et al. (2020)) are available, so that surveys can mask these contributions out.
A non-extensive list of foregrounds can be found in table 1 of (Dickinson (2016)) and in the LAMBDA Foreground review. The brightness of each of these is shown as follows, both in intensity and polarization.
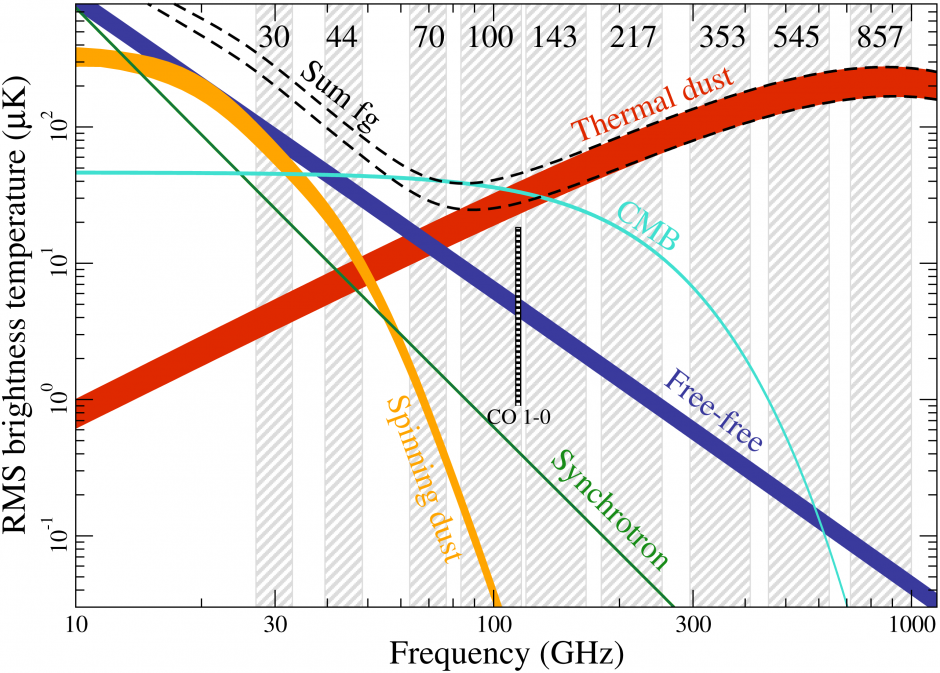
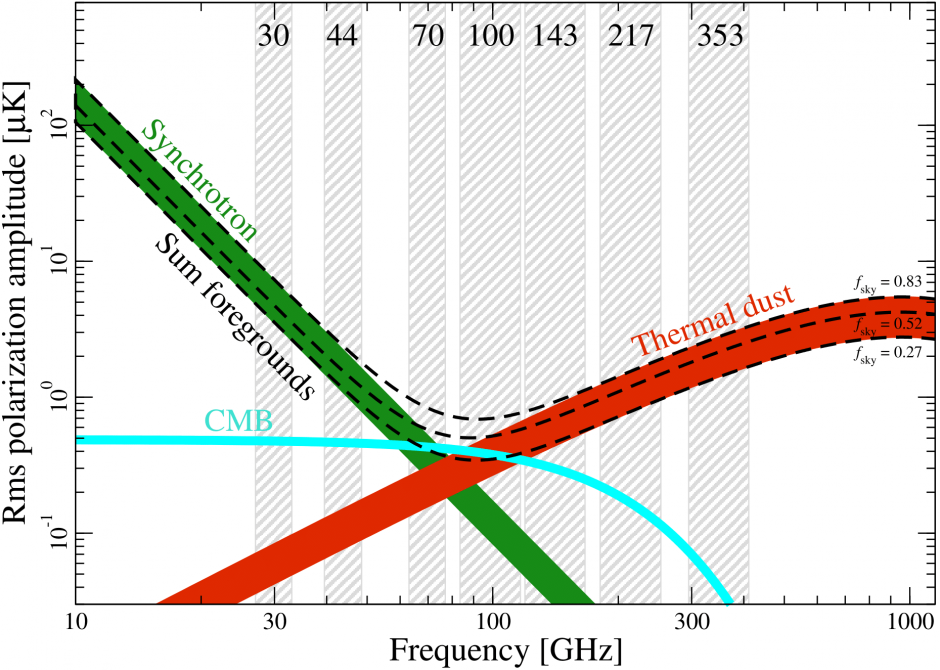
CGEM Observing Band
CGEM will observe in the band of 8-10 GHz. It will obtain high signal-to-noise Stokes Q and U maps of Galactic synchrotron and spinning dust emission. The main cosmological goal of CGEM is to enable improved foreground models in aid of the CMB B-mode polarization search. A secondary goal is to better understand the interstellar medium.
By observing near 10 GHz, CGEM will map these foregrounds at a much higher signal to noise than if they were observed near the CMB window (~100GHz). These maps will then be extrapolated to higher frequency, where they can be used to remove foreground B-modes from CMB data. CGEM will target large angular scales, where the B-mode signal potentially dominates the lensing B-mode signal. In order to aid in the B-mode search, CGEM must have excellent polarization purity.
Accordingly, the feed, system geometry, and the shapes of the reflectors are all being carefully optimized to maximize polarization purity.
An example of the maps that CGEM will produce is shown below. The map shown was produced by WMAP, with an instrument not optimized to measure polarization.